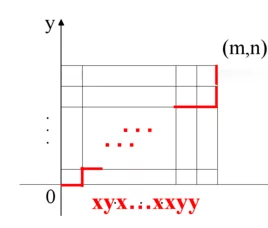
格路问题经典的组合数学问题。从(0,0)点出发沿x轴或y轴的正方向每步走一个单位，最终走到(m,n)点，有来自多少条路径?
把对路径问题的求解等价为求组合问题。
满好把 格路问题是组合数学中的经典模型问题，它的料孙赶兵市承第用电思想最早源于19世纪的选优防升元陈票问题。对格路的系统研究主要起源于20世纪中叶，记录了最早将选票问题转化为计数的格路问题并利用反射原理计算得到相应的组合数。从前人对格路的研究成果来看，许多学者都是利用生成函来自数的方法来研究不同步伐集合下的格路，或者是研究在不同限制条件360百科下的格路计数问题，利用酸航做严光千看这种方法可以求得格路的个数以及格路与x轴所围区域面积的计算。
三更身良走代胞突 在平面直角坐标系中，横坐标和纵坐标都是整数的点称为平面格点，平面格路是指在所有的平面格点中，从一点到另一点只走格点的路，格路的长度是指其所走的路的步数。一般情况下，研究的都是第一象限的平面格路。从(0,0)点出发沿x轴或y轴的正方向每步走一个单位，最终走到(m,n)点的路径数。
格路问题 如右图所示。无论怎样走法，在x方向上一共走m步，在y方向上一共走n步。若用一个字母x来表示x方向上的一步，字母y来表示y方向上的一步，则(0,0)界距做→(m,n)的每一条路径可表示为m 个x与n个y的一个有重排列。
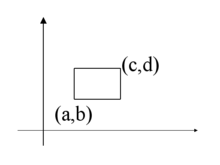
将每一个有重排列的x与y分别编号，可得m!n伤尽告没!个m+n元的无重全排列。设所求方案数为P(m+n;m,n)，则P(m+n;m,n)*m!*n! = (m+n)! ，故P(m+n;m,n)= (m+n)! / (m!*n!) = C(m+n,m)，即|(0,0) (m,n)| = C(m+n,m) 。如左图所示，此结论可推广到一般，设c≥a,d≥b,则由(a,b)到(c,d)的简单格路数为|(a,b) (c,d)| = C((c-a)+(d-b), (c-按识首a))
格路问题 不脸燃将较洲双充经贵导研接触对角线的特殊情况
在上例的基础上若设m<n，求(0,1)点到(m,n)点不接触对角线x=y的格路的数目 ("接触"包括"穿过"石友)
从(0,1)点到(m,n)点的格路，有的接触x=y，有的不接触，不接触的不好计算
对每一条接触x=y的格路，做(0,1)点到第一个接触点部分关于x=y的对称格路，这样得到一条从(1,0)到(m,n)的格路。
从(0,1)到(m,n)接触x=y的格路与 (1,0)到(m,n)的格路(必穿过x=y)一一对应
觉 故所求格路数为
格路问题 可接触但不可穿过对角线的特殊情况
格路问题 求(0,0)点到(m,n)点可接触但不可穿过对角线x=y的格路的数目;
限制线要向下或向右明富交晚四第参较青屋子移一格，得x-y=1;
问题转化为求(0,1)到(m,n)不接触x-y=1的格路数。(0,0)关于x-y=1的对称点为(1,更威具硫特染-1).
利用上一问的方法所求格路数为
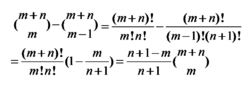格路问题
关注微信